Redução de Dimensionalidade 

Dimensões, imagem do site no link. 

Thiago Bluhm 13 min read 

Existe uma maldição por trás desse tema! Emprega-se os mais variados títulos a este mal que assombra as nossas machine learnings de todo o santo dia. 
Mas, assim como não existe bem que sempre dure, uma maldição pode ser desfeita e para tanto existem algumas estratégias usadas para nos livrar dos efeitos negativos desse interessante mal que nos circunda. 

Observação: Caso você esteja familiarizado com a teoria por trás da redução de dimensionalidade e queira ver apenas o código python enxuto para resolver o output das features com maior taxa de explicação, clica aqui. 

Introdução: 

Quem começou com esta celeuma foi Bellman[1] em 1961, disse ele: 

A maldição da dimensionalidade indica que o número de amostras necessárias para estimar uma função arbitrária com um determinado nível de precisão cresce exponencialmente em relação ao número de variáveis de entrada (ou seja, dimensionalidade) da função. 

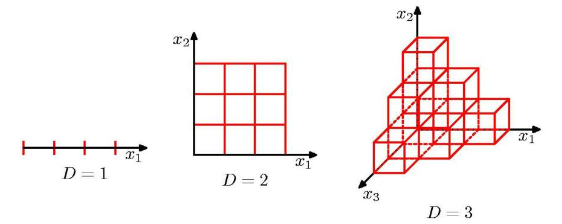
Fonte no link 

Sendo D nossa quantidade de dimensões (variáveis explicativas) percebemos que Bellman estava rogando uma praga, ou melhor, uma maldição há algumas décadas atrás. D1 parece simples demais, vamos para D igual a 2, já vemos um cenário interessante, simples e que pode facilitar nossos objetivos. Ao passo que, adentrando D3 é possível enxergar um ganho de complexidade para determinar uma conexão e/ou padrão entre os dados. 

Permita uma analogia, 

Você está com fome e com pressa e um amigo o convida para irem almoçar em um restaurante que ele gostaria de conhecer, você aceita. Chegando ao restaurante você se depara com o cardápio e com uma quantidade enorme de ingredientes que podem ser utilizados no preparo do seu prato: queijos, presuntos, carnes, verduras, ovos, temperos, molhos, etc. Você pode usar uma quantidade definida de tipos de proteína, outros tantos de temperos e molhos até que toda essa variedade de sabores, cores e cheiros te faz pensar em pegar tudo, jogar na panela e comer. Obviamente a comida o deixará saciado pela quantidade, mas talvez você não tenha aprovado o restaurante. A aquarela de temperos se tornou uma má digestão, pois todas aquelas opções não te deram chance de escolher minimamente bem. 

Opções demais, menos praticidade. 

E assim muitos iniciantes em Ciência de Dados imagina que mais dimensões é melhor para o modelo dando, ao algoritmo de aprendizado de maquina, um leque maior de informações que virão a serem capazes de explicar o seu regressando ( conhecido também como: outcome, y, variável dependente ). 

Todavia, essa variedade pode se tornar algo difícil para o modelo interpretar e chegar a um patrão coerente. Entenda interpretar como buscar padrões suficientes para ter uma boa previsão, caso não tenha ficado claro. Sim, detalhe, sua “pressa” seria o custo computacional para realizar tamanha operação. Deixo aqui mais uma ponta solta no que tange performance de um modelo versus capacidade preditiva. 

Dadas as devidas introduções, espero que tenha captado superficialmente o intuito dessa prosa e que não tenha tido uma indigestão. 

Deixo aqui os créditos do artista 

Keep Holding… 

Então quer dizer que eu não posso ter mais de D dimensões no meu modelo? 

Não é bem assim, não é necessário limitar nossos modelos a um número de dimensões! É preciso avaliar o contexto inteiro para comungar com todas as dimensões que estão disponíveis no nosso dataset. Mais a frente irei falar sobre os Componentes Principais de Análise, PCA. Antecipadamente vejamos abaixo, no gráfico, uma prévia do que iremos tratar: 

A partir de certa quantidade de componentes não explicamos mais Variância. 

Você se pergunta: Certo! E como eu posso reduzir essa dimensionalidade de uma forma que eu saiba quantas features “no máximo” eu devo usar sem comprometer a qualidade do meu modelo? 

A pergunta ainda não é bem essa: quantas features no máximo eu devo usar…? Vamos montar uma melhor: 

Uso quantas features? 1,2,3,4… 

Quantas features eu devo usar para obter um modelo razoável, com redução de erros e controlando os resíduos? 

Observação: Erro e resíduo são coisas distintas. 

MÍNIMOS QUADRADOS (MQO) 

Em poucas linhas, em caráter de importância, é bom comentar sobre o MQO ou mínimos quadrados ordinários. Incondicionalmente nos remete a quantidade de erro que o meu modelo produz, pois é daí que sairá quanto o meu modelo é bom e capaz de resolver o problema de predição. 

Existem diversas boas métricas para avaliar a qualidade do modelo baseado em MQO, poderia citar o: RMSE, MAE, MSE, MAPE. 

Se houve compreensão ao que foi lido até aqui podemos então inferir que mais features, provavelmente, mais erro eu passo a adicionar no modelo. Sim! Provavelmente. 

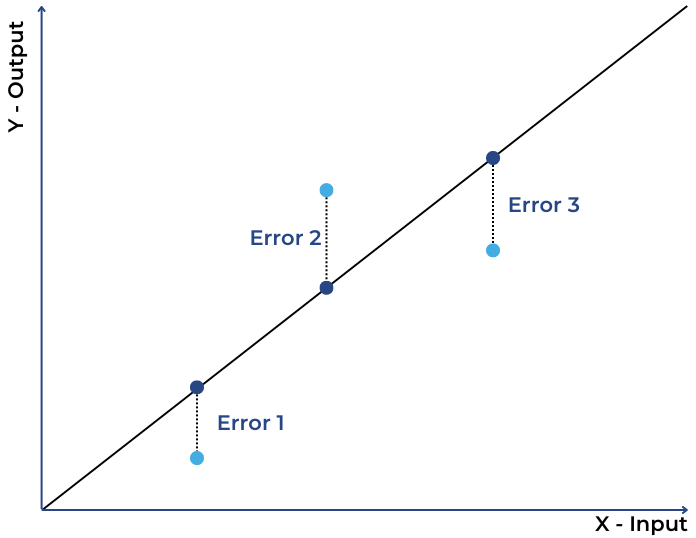
Linha Fit e a diferença dos pontos observados erro de predição geral 

Quais problemas surgem com mais dimensões? 

Alguns tantos aparecem com a alta dimensionalidade: Multicolinearidade, Pontos Influentes, Singularidade, Dependência linear. Outro tópico importante e ficará para outro artigo! 

Desejo um dataset coerente! 

Seu desejo está longe de ser uma ordem. 
O que todo cientista de dados espera ter em um dataset? Um fit razoável, com uma variância bem explicada, resíduos distribuídos próximos a uma normal, homocedásticos e linearmente independentes. Olha esse fit no plot com sns.regplot aqui embaixo: 

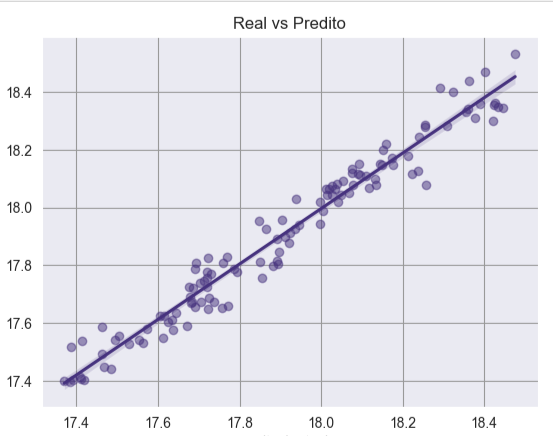
Figura: Fit real com R2 de .90 no teste 

Mas você precisa estar preparado para o pior, modelos com alta quantidade de erro, R2 baixo, resíduos longe da normalidade, auto correlacionados, dependentes linearmente e heterocedásticos. 

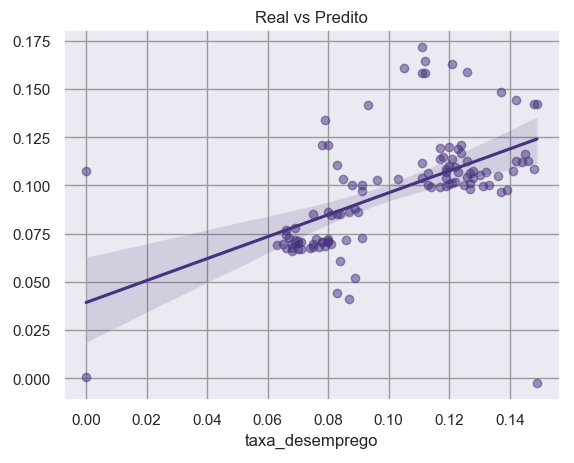
R2 de 0.33 

Então o pulo do gato é reduzir as dimensões a um número eficiente. Sim! 

Jump’s cat 

PCA — PRINCIPAL COMPONENT ANALISYS 

PCA, ou Análise de Componentes Principais (em inglês, Principal Component Analysis), é uma técnica estatística utilizada para simplificar a complexidade em conjuntos de dados de alta dimensionalidade, mantendo as informações mais importantes enquanto reduz a dimensionalidade. 

A ideia principal por trás do PCA é transformar um conjunto de variáveis correlacionadas em um novo conjunto de variáveis não correlacionadas, chamadas de componentes principais. Cada componente principal é uma combinação linear das variáveis originais. O primeiro componente principal captura a maior parte da variabilidade dos dados, o segundo componente principal (ortogonal ao primeiro) captura a segunda maior parte, e assim por diante. Veja o gráfico abaixo: 

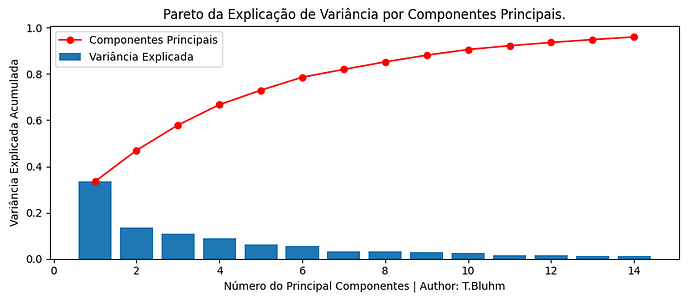
Componente Principal 1 (PC1) explica mais que o dobro do PC2. 

Em síntese, ao calcular os PC’s estou reduzindo a dimensionalidade por que irei ficar apenas com os componentes que explicam mais minha variabilidade. Explicando mais variabilidade eu, provavelmente, poderei ter menos erro no modelo correto. Sim poderá! Não é certeza 100%, mas vale a pena o risco. Vai depender muito dos dados. 

Você então condiciona uma premissa: Ué, mas sendo assim melhor deixar todas as features, pois eu consigo explicar quase 100% da variabilidade… 

Aí é onde entra a questão: alta dimensionalidade pode causar o aumento da complexidade e isso faz com que o modelo perca performance, aumente o gasto computacional e mesmo tendo variáveis que expliquem quase toda a variabilidade podem acarretar outros problemas como os citados anteriormente. A alta dimensionalidade aumenta a sensibilidade do modelo a pontos extremos, podendo distorcer as conclusões. 

Uma bóia salva-vidas 

Socorro! 

Calma, entenda que: ao reduzir a dimensionalidade, estamos, de certa forma, simplificando o conjunto de dados, concentrando-nos nas variáveis mais relevantes. Isso pode ajudar a suavizar a influência de pontos atípicos, melhorando a estabilidade e a generalização do modelo. Vamos interpretar o PCA e demonstrar em números, isso vai abrir mais o aprendizado. 

Interpretar o PCA 

Basicamente, será feito o exame nos loadings das variáveis em cada componente principal, entender quais variáveis contribuem mais para cada componente e decidir quantas componentes reter com base na taxa acumulada de explicabilidade de variância. Quem são os loadings? 

Loadings = Combinação linear das variáveis originais! 

Observando o dataframe abaixo é possível perceber como uma matriz dessas combinações lineares, loadings, são visualizados. Veja a imagem abaixo: 

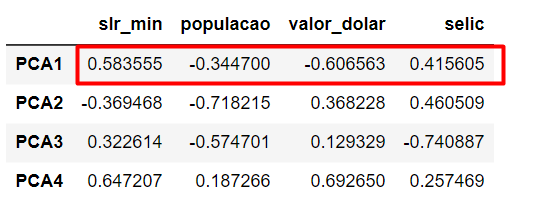
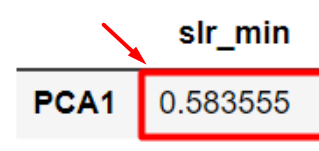
PCA1 tem loadings mais altos para [slr_min, selic] 

Agora vamos nos deparar com os autovalores e os autovetores que geram os componentes principais. Permita-me usar no restante do texto os termos eigenvalues para autovalores e eigenvectors para autovetores. Abaixo o trecho do script para capturar os eigenvalues e eigenvectors e mais a frente no texto será possível encontrar o script completo, por hora o externado aqui nos basta, veja: 

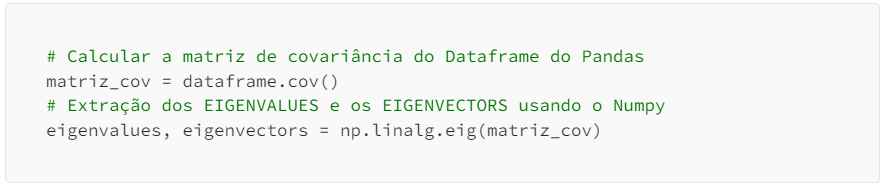
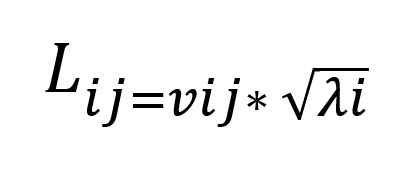
Matematicamente o Loading 

• Lij​ é o loading para a j-ésima variável no i-ésimo componente principal. 
• vij​ é o j-ésimo elemento do i-ésimo eigenvectors. 
• λi​ é o i-ésimo eigenvalues. 

Demonstrando rapidamente como chegar no valor de um loading: 

Você: Ok! E como chegamos então ao componente principal? 

_Python_(): 

Perceba que essa fórmula implica que os loadings são proporcionais aos eigenvectors, mas também são ponderados pelos eigenvalues associados.​​ Os eigenvalues indicam a quantidade de variância explicada pelos componentes principais correspondentes, e os loadings indicam a contribuição relativa de cada variável para o componente principal. 

Como dito anteriormente: 

Você: Ok! E como chegamos então ao componente principal? 

_Python_(): 

Usando Python para calcular os componentes principais e extraição dos eigenvalues e eigenvectors. Usarei um Pandas Dataframe com variáveis econômicas, sociais e industriais retiradas de diversas fontes, como por exemplo o IBGE. 

Boa dica para tirar amostras de dataframes usando .sample(frac= valor da fração ) 

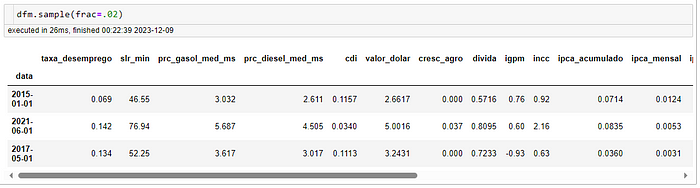
Tirando uma amostra de 2% do dataset 

Vamos usar a padronização com o StandardScaler(): 

Irei padronizar os valores das séries(colunas) do dataframe para conseguir processar os componentes principais. Guardarei o fit para posteriormente, caso eu queira, possa usar o inverse_transform(). 

Início do Script Python: 

Eigens capturados: 

Os eigenvalues são retornados como uma matriz, e os eigenvectors são retornados como uma matriz onde cada coluna representa um eigenvector. 

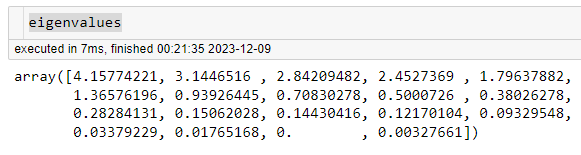
eigenvalues 

Os eigenvectors são ordenados de acordo com os eigenvalues, e os primeiros eigenvectors (os “principais”) são escolhidos para formar um novo conjunto de bases. 

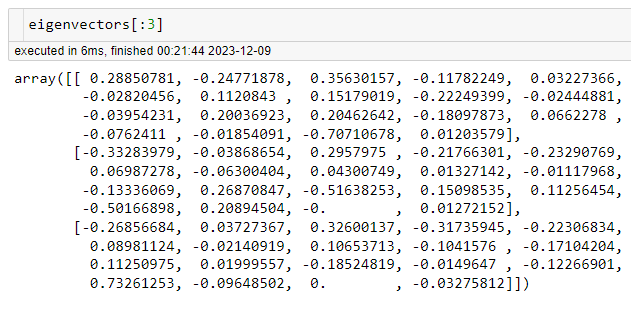
Autovetor 

Agora os Componentes Principais: 

Os componentes principais podem ser obtidos multiplicando os eigenvectors pelos eigenvalues correspondentes. A ordem dos eigenvectors é determinada pelos eigenvalues, com os eigenvectors correspondentes aos maiores eigenvalues sendo estes os primeiros componentes principais. 

Atenção! Veja que a quantidade de Componentes Principais é a mesma de colunas do dataframe, ou melhor, mesma quantidade de features do dataframe original, confere? 

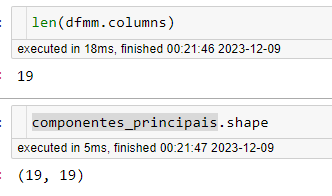
19×19 

Ou seja, cada Principal Component (PC), é uma combinação linear… 

Vale a pena entender essa combinação, pois cada feature do dataframe original será transformada em um valor de contribuição, no caso os loadings que foram demonstrados anteriormente no texto. Vou fazer um slice dos 3 primeiros PC’s, cada valor dentro de cada uma das matrizes abaixo é representa a combinação linear com o componente: 

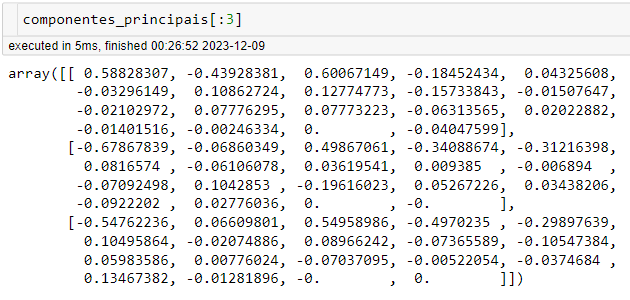
Já que a ordem é simplificar… vamos desenhar então, ou melhor, plotar! 

Fica mais inteligível oferecer graficamente o nível de contribuição de cada feature dentro do PCA1, PCA2, … PCAn: 

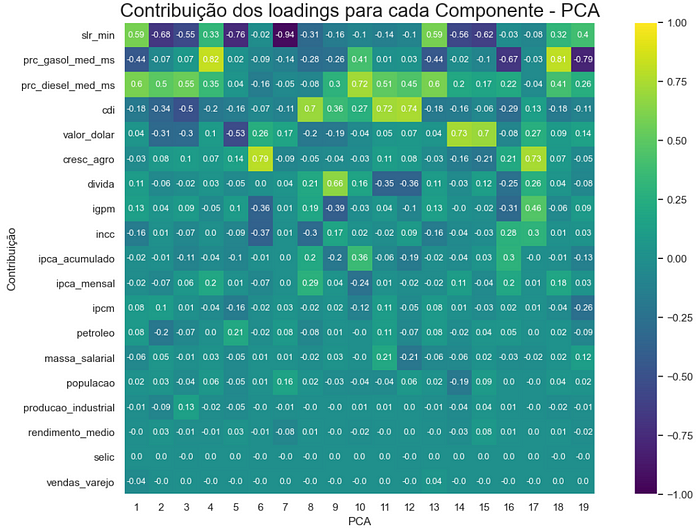
As regiões mais claras indicam mais contribuição 

Vendo os números em um dataframe onde o índice são os PCA’s: 

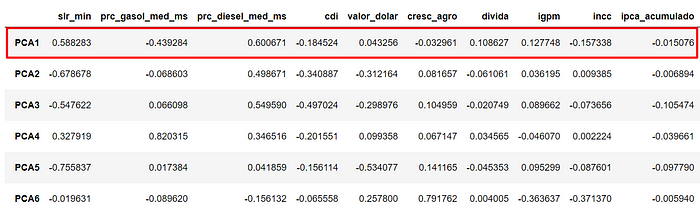
Basta conferir com o gráfico matriz acima 

MATRIZ COM OS PC’s COM A MAIOR TAXA DE EXPLICAÇÃO DE VARIÂNCIA: 

Já é possível reduzir a quantidade de dimensões e ficar com os PC’s que explicam X% da nossa variância. Parece que assim temos algo muito interessante. 

Observação: Neste artigo fica proposto o valor de 95% de explicação de variância. 

Para fazer isso é preciso capturar o array com os nossos eigenvalues e dividir cada um deles pela soma de todos os eigenvalues: 

Com 10 de 19componentes eu explico 95% da variância 

Um plot ajuda muito +++ : 

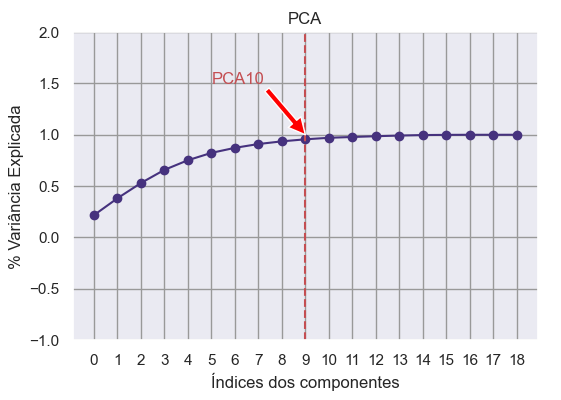
Ponto de corte no PCA 10 

É percebido que, ao atingir o número de 10 componentes, a explicabilidade de variância atinge um platô de performance e nesse local reside o “cutoff” ou, famigerado, ponto de corte. 

Até aqui conseguimos assistir em detalhe como retirar os componentes principais, calcular seus gerados com a decomposição dos eigenvectors e eigenvalues. 

Contudo como aplicar isso em uma Regressão Linear e tentar estimar uma boa previsão? 

Então faremos uma breve estimação utilizando uma Machine Learning baseada em PCA e Regressão Linear Multivariada utilizando o método dos mínimos quadrados ordinários, MQO. Segue: 

Regressão Linear Multivariada & PCA 

Depois de fazer passo a passo o caminho até os PCA’s e capturar os pontos com maior contribuição para explicar a variância do modelo será usado um pacote python para simplificar os passos daqui pra frente. Ajustar-se-á um modelo baseado em PCA’s. 

Optou-se pelos modelos GLM( generalized linear models ) da Sklearn por ele ser mais conhecido pela maioria e também para trabalhar com a PCA. 

A título de sugestão ver o pacote statsmodels, vale a pena conferir, contudo esta preferência vai de cada um. Segue abaixo os novos scripts: 

O resultado, X_transf, é uma matriz em que cada linha representa uma observação transformada nos novos eixos principais. A quantidade de colunas nesta matriz será igual ao número de componentes principais que você escolheu reter durante o ajuste do modelo PCA. 

Essencialmente, o método transform projeta os dados originais no espaço dos componentes principais, proporcionando uma representação de dimensionalidade reduzida dos dados originais. Este novo conjunto de dados transformado pode ser usado para treinar modelos de machine learning ou para análise posterior. 

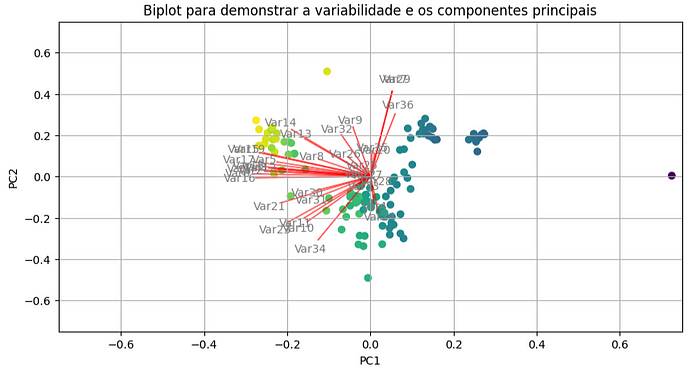
O gráfico propõe na linha vermelha os eigens 

Continue o código com o script abaixo tratando um dataframe: 

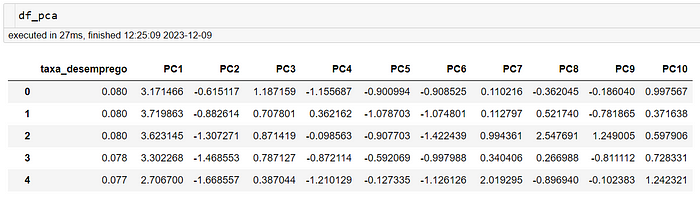
O dataframe composto com os componentes principais 

ENFIM O MODELO: 

Um resultado bem razoável 

Conclusão 

Resolvi boa parte dos problemas relacionados à qualidade do modelo e a confiança que posso ter nas análises. Modelos com alto R2 muitas vezes não dizem muita coisa, apenas que está sendo explicado a um determinado nível e basta retirar uma feature ou colocar outra o R2 é alterado. 

Depois da estratégia de redução com PCA eu sanei o problema de multicolinearidade, os resíduos conseguiram uma distribuição próxima da normal e com homocedasticidade. Foi aferido pelo teste Durbin-Watson que não há autocorrelação entre os resíduos. 

Contudo não deixe de fazer testes nos resíduos, em breve farei um artigo sobre qualidade e será muito focado nos resíduos. Até breve! 

That’s all folks! 

Chegamos ao fim deste artigo, espero que tenham gostado do passo a passo até aqui. Eu sei que o assunto é bem denso, mas tentei deixar mais leve cada pedaço das explicações. 

Agradeço a cada um de vocês que dedicou seu tempo precioso para ler, refletir e absorver as ideias compartilhadas neste artigo. O processo de criar e compartilhar conhecimento é verdadeiramente enriquecedor, e é a comunidade de leitores que torna essa experiência significativa. 

Até nossa próxima!